Jensen Harris from the Office 2007 design team gave a very rare presentation at Microsoft’s MIX08 event today about not what the Office 2007 Fluent (Ribbon) interface is about, but instead how it came to be and what other concepts they tried.
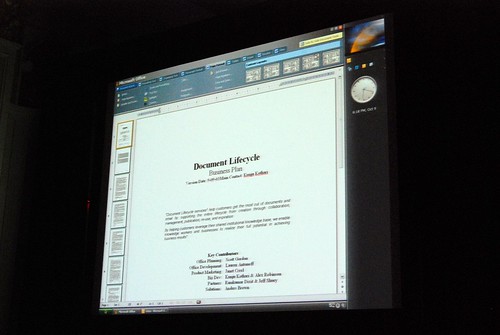
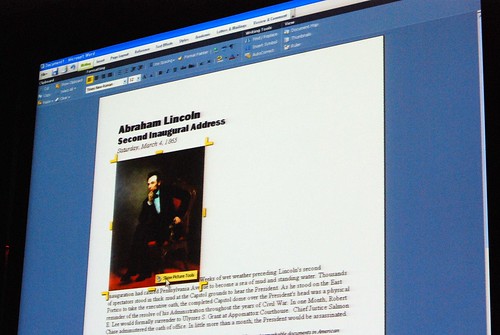
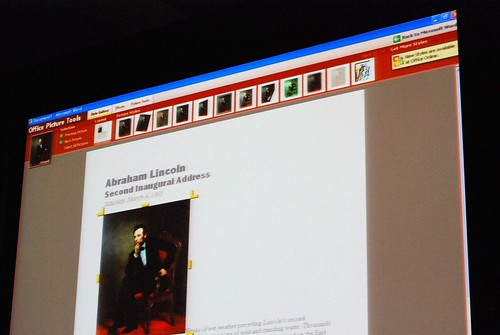
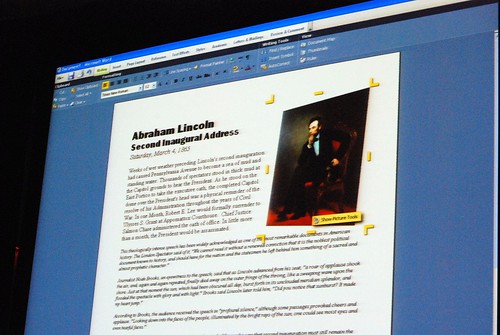
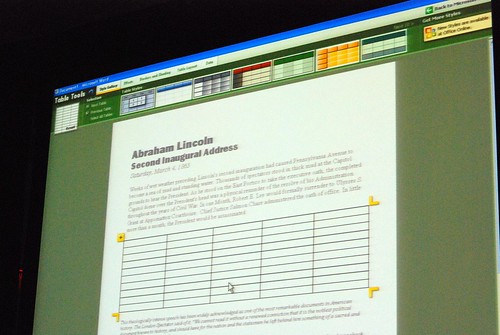
He admitted himself it was the first time ever in a public venue where they’ve shown these never-before-seen prototypes of what would become Office 2007. It was great insight into the development process of Office which frankly may not have been very interesting except the last release. Having said that, it was still a very small selection of material out of the 50-60GB worth of prototypes Jensen claims have been archived.
Most of these were presented in sequential order so it was also interesting to see how the design evolved.
It will be another 24 hours before the session recording will be uploaded to the MIX website, but I highly recommend everyone to check it out when it is available to hear Jensen had to say about each slide.
Comments for "Office 2007 interface prototypes"
tino
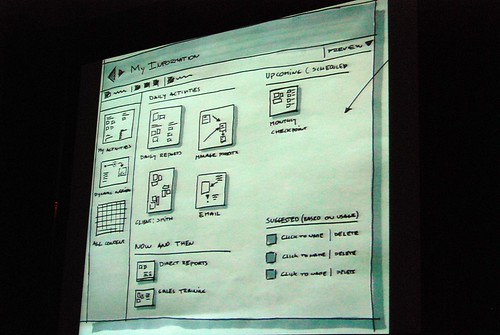
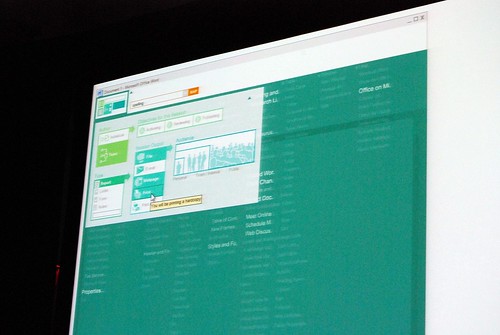
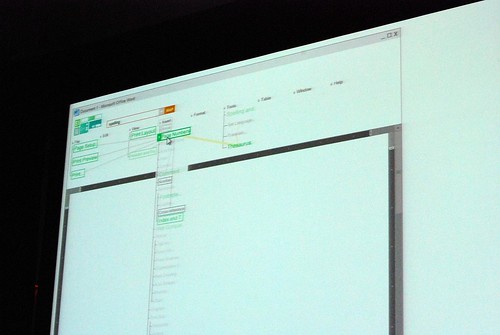
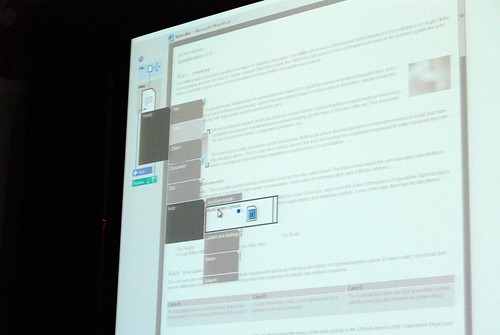
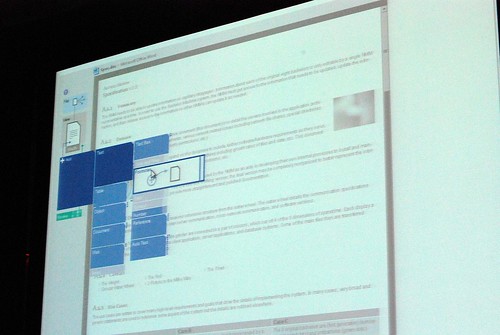
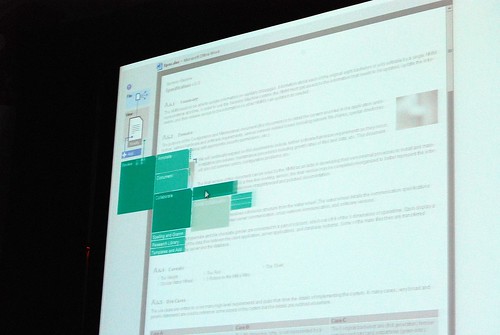
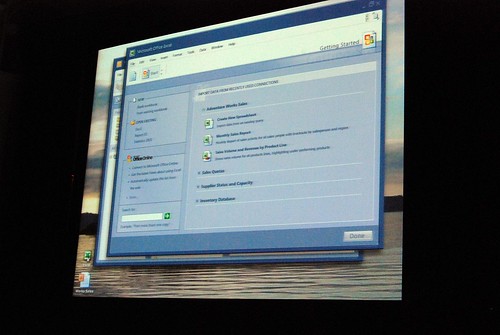
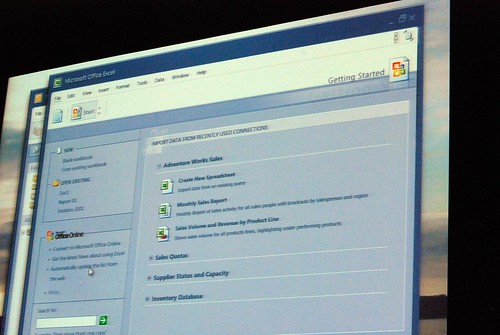
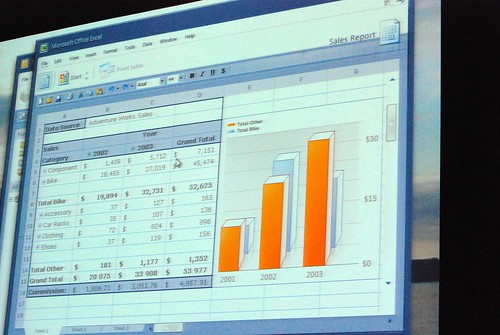
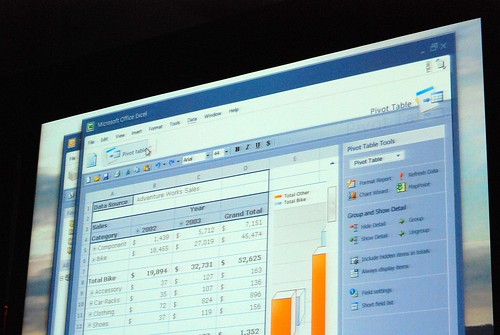
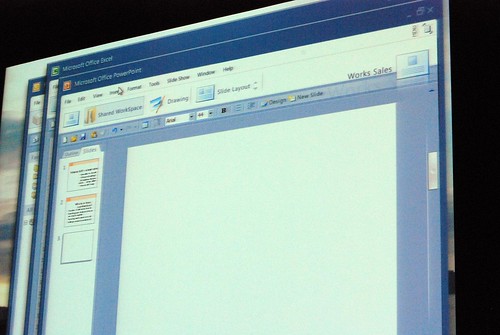
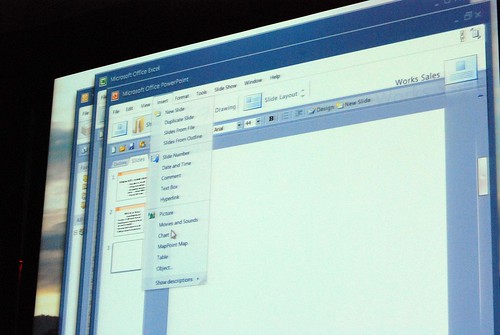
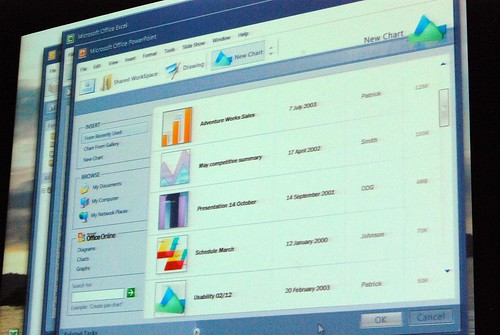
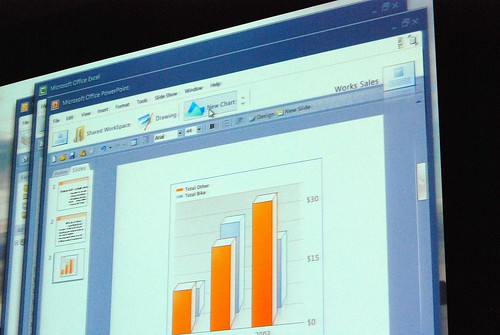
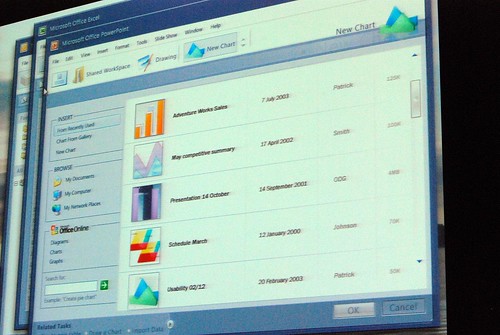
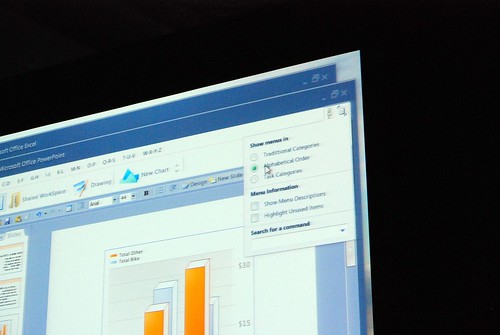
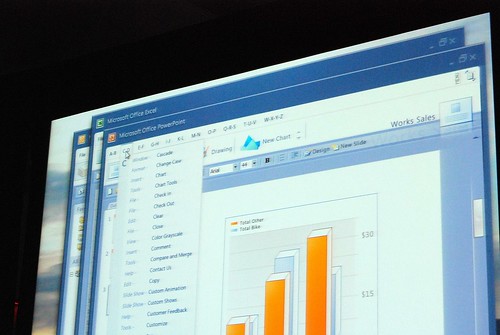
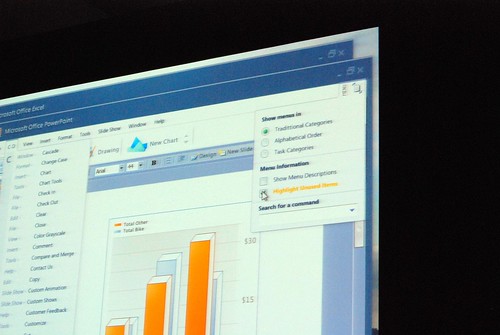
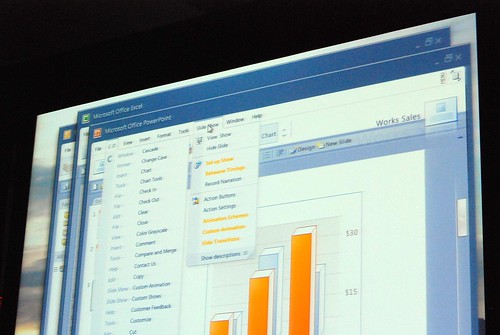
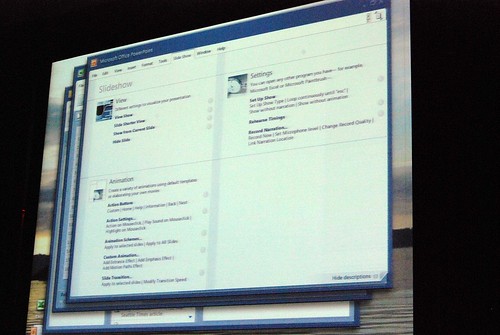
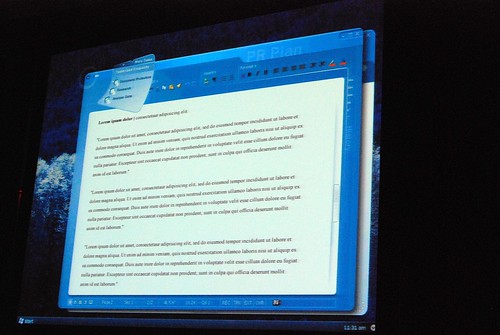
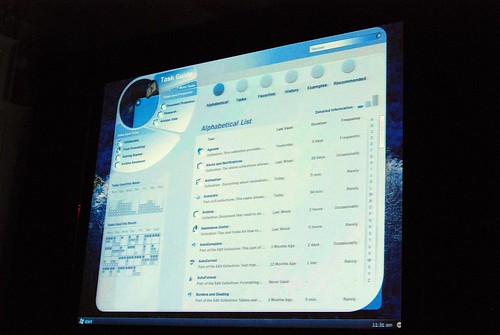
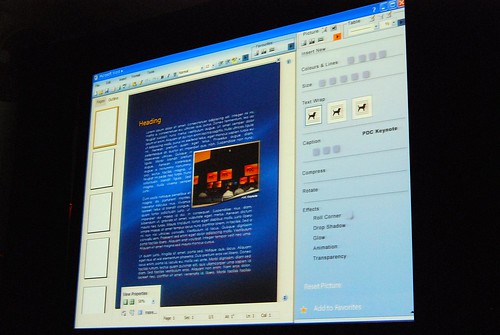
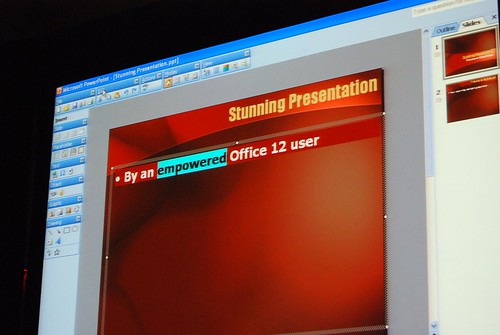
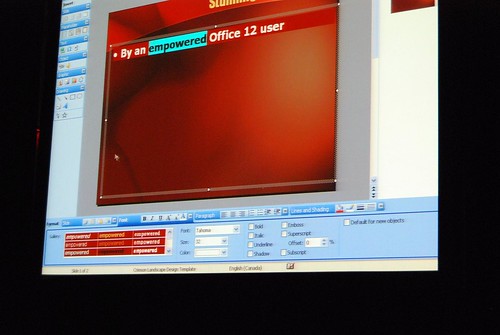
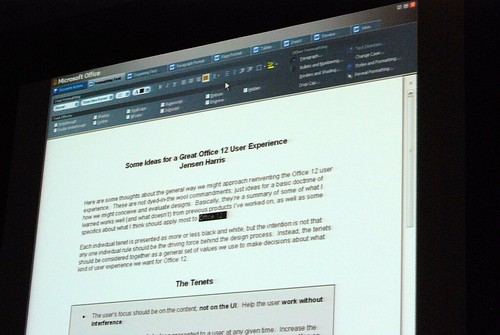
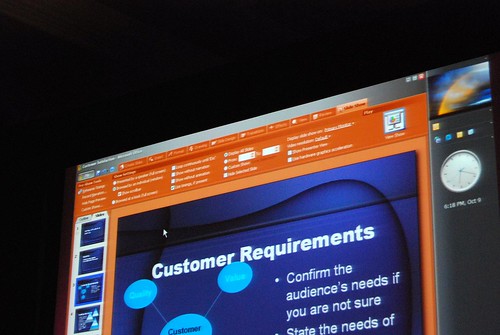
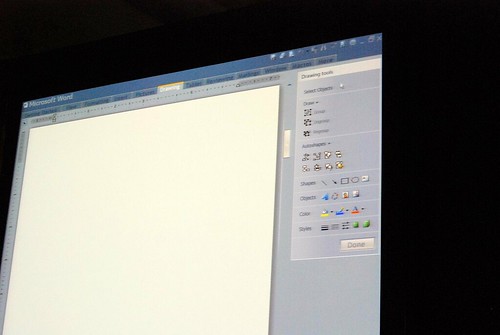
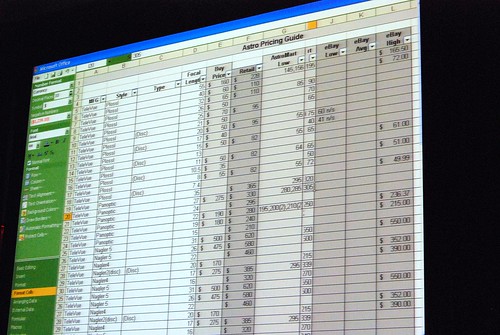
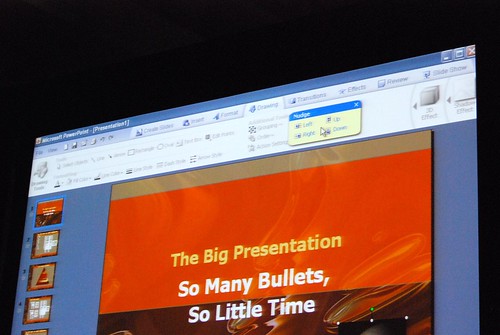
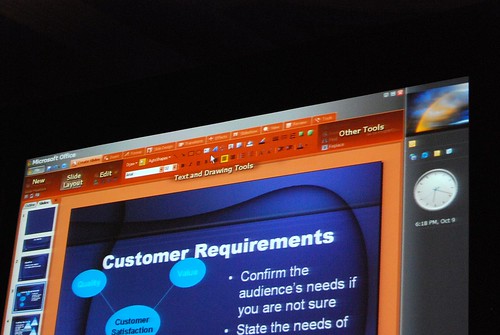
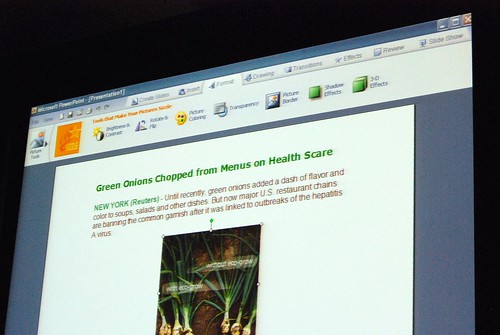
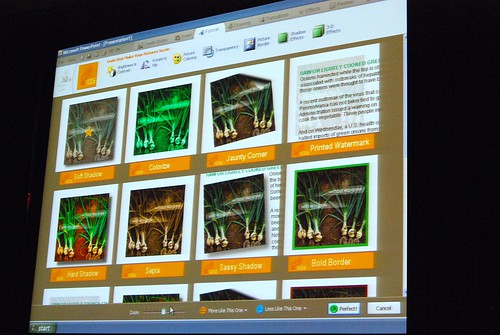
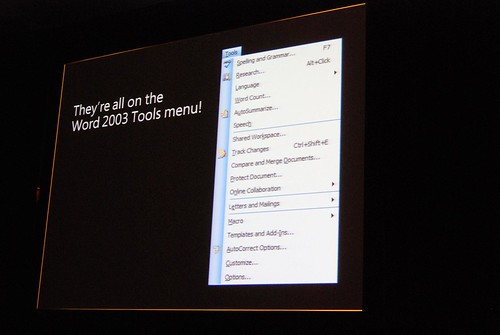
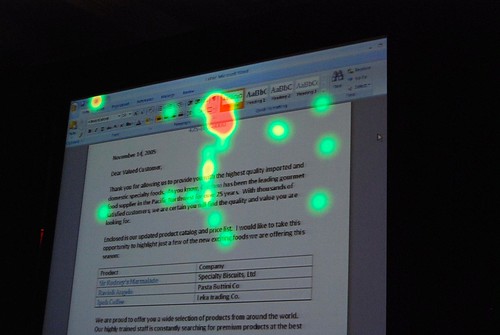
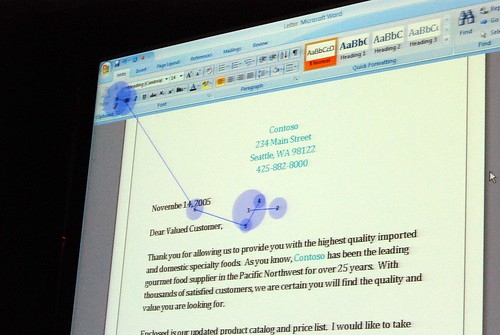
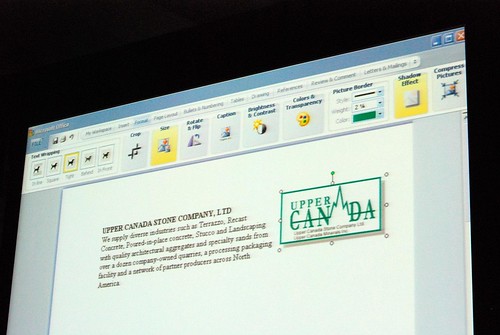
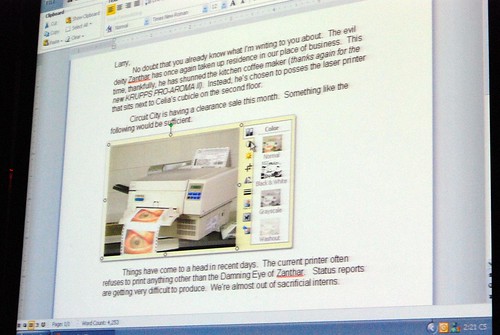
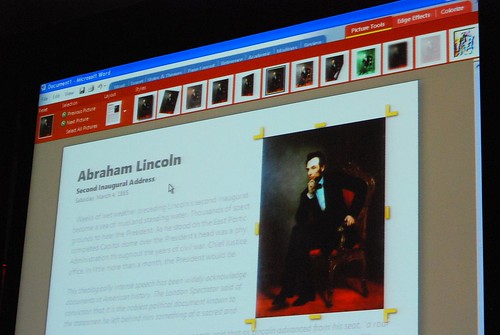
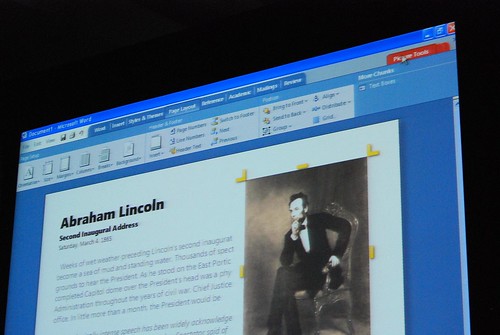
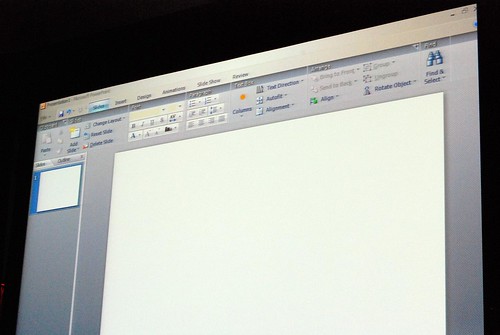
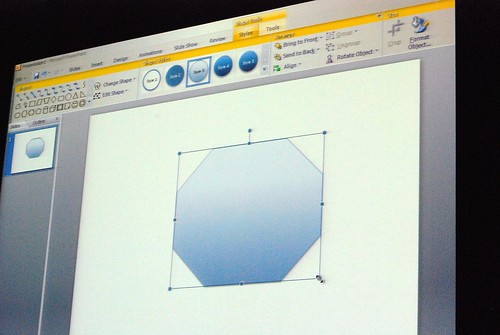
Very interesting stuff!
So thank you. There are a lot of smart ideas that they could hopefully implement in some way or another into other products (I think of a new Paint and WordPad for Windows Seven)
Garion
Wow… I’ve submitted this to digg, so those with an account, please digg it.
@tino - I believe that this team is in charge of coming up with a new Windows Explorer for Windows 7
http://digg.com/microsoft/Pics_Office_2007_interface_prototypes
Justin
some of those they dropped along the way look better and easier to work with… but learning that the current ribbon ui that i’m using is coming from a lot more effort than i thought makes me appreciate it more…
Anthony
WOw some of the ui accurately reflects the look from early longhorn builds. I do hope Windows7’s experience and development will be as practically and systematically thought out like Office12.
Raiker
Great stuff
by the way, records of the sessions (prototypes demos included) are already available:
http://msstudios.vo.llnwd.net/o21/mix08/08_WMVs/UX08.wmv - Beneath the Surface
http://msstudios.vo.llnwd.net/o21/mix08/08_WMVs/UX09.wmv - The Story of the Ribbon
Claudio
Being able to follow a creative process of such size is always nice! I wonder what kind of methodology they follow in developing UI. Anyone has a clue?
ikyouCrow
i still prefer the brushed metal look for Office.
i wonder if they’ll ever release a visual style for XP or Vista with that appearance? i can’t be the only one who’d want to use that. especially if they put the various colours in there too. like the Word blue, and the Excel green, and the Powerpoint orange….
steveballmer
The Apple people come here to steal our ideas!
Short Zheng
Where’s ‘Try 3′?
David
It was interesting to note at the end that Jensen Harris made reference to ‘Scout’ (http://www.istartedsomething.com/20070907/office-search-commands-demo -jeff-scanlon/) possibly showing up on Microsoft.com in the future. The relevant section of the video (linked to by Raiker above, UX09.wmv) is at 1:25:18 onwards. He talks about some of the problems including a search function (language issues, etc.) - it’s worth listening to.
rożen
This is precisely something that opensource fanboys will never understand - that the cruel “micro$oft” spends lots of time and money on UI research. MS ideas get copied by opensource geeks five years later, as they try to catch up with Windows XP (yes, KDE introduced the “new removable media insterted, what do you want to do with the files” dialog six years after XP and they marketed it as an “exciting breakthrough”).
Raiker
Also presentation itself is available for those, who are excited: http://msstudios.vo.llnwd.net/o21/mix08/08_PPTs/UX09_Harris.pptx
sdf
Я ебу чо напридумали! Ужоснах!!
хотя привыкнуть можно.. гыгы
Andre F.
@sdf
Ти с кем разговариваеш?
Hok
The last picture was the one I get on beta 1.
Matt Sharpe
Very interesting, thanks!
unbreakable
The ribbon stinks big time, and these stupid designs show why it stinks big time…
they wanted to make something different just for the heck of it and failed so bad its funny.
The ribbon is an abomination of design, they should at least lett a fall back option for classic toolbars (something that a 3rd party had to build and sell!).
This ribbon along with the vista start menu and the new interface for windows explorer I can say without regret, that they seem to be build by monkeys….
Hot tracking is not enough… good idea but you should have tested further with other ways… sigh…
Chocolate
Very nice screenshots. Last foto is interest for me. Very nice graphics possibility
Marconi
In some steps, it looks like Lottus Symphony.
Fedex Ultra
Good pictures!! I really like those prototypes, specially does before the “How different should it be?” slide. Thanks!!
Kolgoth
@unbreakable: Personally, I like the ribbon interface over the classic toolbar option. My reasons why?
Simple! I can fit a lot more functionality that’s easily recognizable and dynamic in the ribbon toolbar setup than I can in a classic toolbar setting. I can also hide and show the ribbon, thus maximizing my usable screen real-estate without a whole lot of fuss. It was a real pain to try to do the same thing in the toolbar setup. Now it’s the press of a simple hotkey and BOOM!
Another benefit is the dynamic nature of the ribbon - another aspect that has proven to be very helpful to me versus the classic toolbar of old.
Mike
I too hate the Ribbon. There are those that have accused me of being resistant to change, but that isn’t the case. I don’t mind change when it is a true improvement, but when that change makes things more difficult and confusing to use the software, that is NOT an improvement.
I use software to get things done, and after nearly a year of trying it, I still cannot be nearly as productive as in previous versions, or in OpenOffice.org. Notice how much effort they seemto have spent trying to make a different user interface? I want useful, stable features, not to have to spend time figuring out where they hid things on me (and because any new things they add in the next version of Office will need to be in you face, they’ll doubtless shuffle things around in the ribbon again, and you’ll have to find them all over again — what a time waster).
The Ribbon is completely counter to the way I work. If they would allow switching to the old interface if users prefer, then people could still get things done AND use any new features added. So far, I haven’t seen any USEFUL new features added.
My $0.02.worth
Motorbikematt
The Ribbon is awful, and represents change for the sake of change, rather than the sake of increased functionality. The problem seems that Microsoft’s focus was to make it look prettier, instead of just improving some of the stupid interface and functionality bugs that existed in previous versions. In fact, it appears that many of the old problems still exist, which means that more money was put in the art department than was put in the underlying functionality department. The fact that they didn’t offer a way to go back to the old UI is just mind boggling.
Also, to respond @Kolgoth, if you want full screen in Word 2003, just hit Alt+V, then U, or just make your own shortcut.
Leave a Reply
Microsoft News Weblog » Blog Archive » Office 2007 interface prototypes
[...] [ Long Zheng’s Blog [...]
Exclusvo: Jensen Harris apresenta conceitos do novo Office! « DeskMundo
[...] Fonte e mais informações: istartedsomething [...]
Livebetas.net » Blog Archive » Protótipo de Office 2007 ou Office 14?
[...] imagens: Istartedsomething Ultimas Noticias de Bruno SilvaProtótipo de Office 2007 ou Office 14? - 9 March 2008[EXTRA] - Pack [...]
Las GUIs de Office 2007 que no fueron
[...] Vía | WinBeta Imágenes | Galería propuestas de interfaz para Office 2007 [...]
Tecnologia » Blog Archiv » Las GUIs de Office 2007 que no fueron
[...] Vía | WinBeta Imágenes | Galería propuestas de interfaz para Office 2007 [...]
Las GUIs de Office 2007 que no fueron | Software y Freeware
[...] Vía | WinBeta Imágenes | Galería propuestas de interfaz para Office 2007 [...]
Productividad: El desarrollo del interfaz de Office 2007 - Bitelia
[...] Office 2007 interface prototypes. ← Anterior | Inicio Comparte esta anotación [...]
Los textos de qweos.net» Blog Archive » Office 2007
[...] del 10 de marzo de 2008: de nuevo, Jensen Harris ha mostrado en la conferencia MIX’08 algunos prototipos de interfaces que estuvieron barajando para Office 2007. Muy gráfico e [...]
Las GUIs de Office 2007 que no fueron | YouZone!
[...] Imágenes | Galería propuestas de interfaz para Office 2007 [...]
Office 2007 y las interfaces archivadas | Programas gratuitos
[...] | Genbeta Enlace | Galería de propuestas de interfaz para Office 2007 Enlace | Galería fotográfica del Mix ‘08 record_view_ids(array ( 0 => ‘1649′, 1 => [...]
backdraft » Blog Archive » Office 2007 : prototipos de interfaz de usuario
[...] Long Zheng publica numerosas vistas de esta presentación, bordes redondeados, uso del lápiz de toda la vida al comenzar, eyetracking, uso de barras laterales o controles flotantes son parte de las ideas mostradas.Via Bitelia [...]
links for 2008-03-11 « My Weblog
[...] Office 2007 interface prototypes - istartedsomething (tags: microsoft office process interface usability design gui) [...]
Jensen Harris: An Office User Interface Blog : The Story of the Ribbon
[...] are photos of the beginning and the end of the talk courtesy of Long Zheng. (You’ll have to watch the presentation to see what’s [...]
MSDN Blog Postings » The Story of the Ribbon
[...] are photos of the beginning and the end of the talk courtesy of Long Zheng. (You’ll have to watch the presentation to see what’s [...]
Office 2007 käyttöliittymän prototyyppejä « C:>dir *.*
[...] kuvat: http://www.istartedsomething.com/20080308/office-2007-interface-protot ypes/ Explore posts in the same categories: [...]
Office “Scout” Search Commands makes IEBlog cameo - istartedsomething
[...] Office 2007 interface prototypes [...]
Microsoft News Weblog » Blog Archive » Office “Scout” Search Commands makes IEBlog cameo
[...] Speaking at the MIX08 conference last week, Jensen Harris of the Office design team also made a subtle reference to Search Commands when answering an audience question and said to keep an eye out for it on Microsoft.com “soon”. [...]
Microsoft shows off Office 2008 interface prototypes
[...] [Source: I started something] [...]
212 Blog » Blog Archive » Design and Prototyping of Office 2007
[...] Here’s a collection of interesting photos from a Microsoft presentation about the design and prototyping of Office 2007. My favorite slide though has to be this one: Its probably the most concise description of an interative design process I’ve seen. Office 2007 interface prototypes - istartedsomething [...]
rascunho » Blog Archive » links for 2008-03-14
[...] Office 2007 interface prototypes - istartedsomething Jensen Harris from the Office 2007 design team gave a very rare presentation at Microsoft’s MIX08 event today about not what the Office 2007 Fluent (Ribbon) interface is about, but instead how it came to be and what other concepts they tried. (tags: http://www.istartedsomething.com 2008 mes2 dia14 at_home usability apresentação prototype Office gallery ****) [...]
Protótipos do Office 2007
[...] Link da página (e fonte no mesmo link): Office 2007 Prototypes - istartedsomething [...]
Office 2007 Prototype History
[...] MIX08 [via istartedsomething] [...]