Since LiveSide didn’t take the design mockup I did yesterday, I thought I should re-use the flare element for something else.
So I did and made these wallpapers. And like a good wallpaper is suppose to be, there’s no branding, no copyright and certainly no watermark. Just like if you made it yourself. And one of my personal requirements was that it was clean enough to draw on with Ink Desktop, which I use a lot on the tablet.
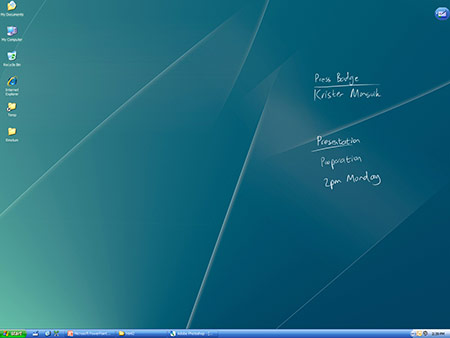
So here they are:
Download 1024×768 resolution
Download 1280×800 widescreen resolution
Download 1280×1024 resolution
Download 1400×1050 resolution
Download 1600×1200 resolution
Download 1680×1050 widescreen resolution
Download 1920×1200 widescreen resolution
Download 2560×1600 30″ LCD widescreen resolution
Also added a sea-blue version:

Download 1024×768 resolution
Download 1280×800 widescreen resolution
Download 1280×1024 resolution
Download 1400×1050 resolution
Download 1600×1200 resolution
Download 1680×1050 widescreen resolution
Download 1920×1200 widescreen resolution
Download 2560×1600 30″ LCD widescreen resolution
What desktop stickies program are you using? And if it’s a tablet, would you please tell me what its name is?
@k: I am using a program called Ink Desktop to draw onto the wallpaper. You can find information and a download link on this page: http://www.microsoft.com/windowsxp/downloads/tabletpc/experiencepack/overview.mspx
Very nice, thanks Long
Thanks Long.. Using it right now!
Thank you very much.
very nice work, thanks Long Zheng
Hello Long, nice wallpapers.. Is there any alternative to Ink Desktop for Vista? I was unable to install the thing from your link on Vista. Thanks!
@rajo: I wondered about that too. Ink Desktop doesn’t work on Vista as of yet, but I can safely assume they will be developing similar PowerToys for Vista. Nothing official as of yet.
Awesome wallpapers, Long!
These are really nice wallpapers, thank you for sharing.
There’s just one Version missing 🙂 1920×1200
Very erotic Walls!
You know what I’d like to see? A quick tutorial on how this was drawn.
Me love you Long time.
Slick looking long, you’ve got me sold.
@Stan: 1920 coming up.
@Rowan Lewis: If you think about it from the simplest way possible, it is quite easy to draw. In fact, so easy that if I post a tutorial, it’d make these wallpapers look silly. 😛
I wonder if a similar program to Windows XP exist? Would be cool to be able to draw notes on the Windows XP desktop.
@Rane: This is a Windows XP application 🙂
http://www.microsoft.com/windowsxp/downloads/tabletpc/experiencepack/overview.mspx
Well it says it cant install cause it requires the XP Tablet Edition.
Long, put up a tutorial man. 😀 I want to know how this is done.
(yea I copied the comment from Neowin…I really want to know :p)
Very cool, using it now!
awesome Long, thanks again!
Sweet wallpapers, Long. How’d you make your icon text transparent with ink desktop enabled?
@jmc: It’s not transparent. You just pick a color very close to the actual desktop image in the Desktop control panel.
Can you upload a lavender or refreshing light violet version please. I love its simplicity..
Thanks